The International editions of Reader’s Digest (including Valitut Palat, Sélection, Det Beste, Het Beste, Seleções, Selecções, Selecciones) feature logical puzzles created by PZZL.com. Below is explained how to solve them.
The Rules: Draw a line from each number to an outlet. Each line passes through as many spaces as the number indicates. Diagonal, overlapping or intersecting lines are not permitted. Not a single space should be left empty and every outlet should have a number connected to it.
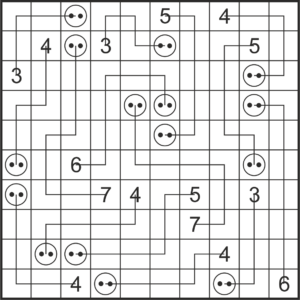
As you can see there are only right angles, no empty spaces, and every number is connected to an outlet through exactly that number of spaces. Most importantly, do not draw in a line unless you are 100% sure it belongs there!
NO EMPTY SPACES
Start with the corners
Since no spaces remain empty, lines can be drawn in all corners. At the top left, this is only possible by connecting the 3 to the outlet in A3. Since A3 cannot be connected to A4 anymore, that space can only be connected to the 3 in B4. And we can extend that line to B6.
At the top right we are not so lucky: there the line can still run from the 4 to C9, or from the 5 to D9. But four spaces are already certain, so a line can be drawn there. At the bottom left the 4 is enclosed, so its line has to go through corner J1 to G1.
The 3 in G9 can only be connected to J8 due to its length, so the 6 must run from J10 upwards. We then filled in the pieces of line that are certain. This makes it clear where the 4 in I8 is headed . . .
ODD OR EVEN
An even connection remains even after a detour
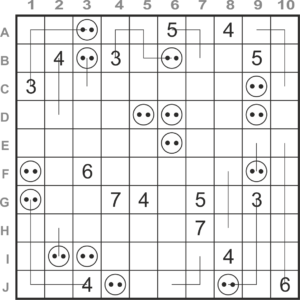
The shortest route from the 8 in E9 to outlet G5 is 5 squares. This means the two can never be connected, taking a detour it becomes 7, 9 or a higher odd number, but never an even 8. Try it!
From this it follows that outlet A1 cannot be connected to the 6 in D2 (would be 3, 5, 7 or longer), so the line can only run to the 3 in C3 or the 8 in E6.
The 4 at top right is 3 spaces away from outlet B7, so it cannot be connected to it in any way, and must therefore run to outlet D8. The 2 in H9 cannot be connected to outlet J8 via I8, because then J9 would remain empty. The other lines follow from the foregoing.
ENCLOSED AREAS
Counting helps
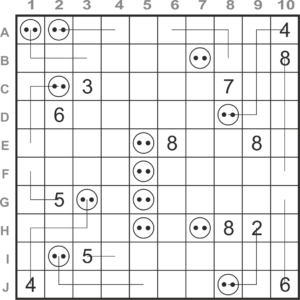
At the top right spaces B10 and C10 are completely surrounded by numbers or outlets. Since there is a line in every empty space, a line of 2 spaces must be drawn here, so from C9 to A10. The 5 in B9 must then run to outlet B5, and not via B6, otherwise A5 would remain empty.
At the bottom right is an enclosed area of 11 empty spaces. Here lines can be drawn from the three numbers 4, 5 and 6. To arrive at 11, the 5 and 6 must be used. It is a bit of a puzzle but there is only one solution.
At the bottom left we can fill three spaces right away. If outlet I2 were connected to the 3 in J3, the 4 in H2 could no longer be connected to an outlet. So the line runs from the I2 outlet via J2, J1, I1 and H1 to the 4 in H2.
EVERY BIT HELPS
Step by step you will come a long way
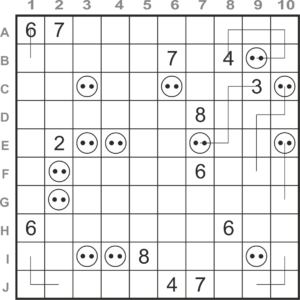
At first sight this puzzle looks difficult. Some things can be filled in at the top right, but apart from that . . .
At the bottom left however, an area of three empty squares J3, J4 and J5 is created after filling the corner. Because there is no 3 anywhere, that line must continue to the 8. And from the 8 it can only end in G2.
The 6 in H1 is now locked in and must therefore go up to at least D1. But now the 2 in E2 is locked in, so it goes up. Which means the 6 has to go up again, which in turn has consequences for the 6 and 7 at the top left.
The same principle can be applied to outlets I3 and I4. Both are locked in and have to go up. Which means I3 has to go up one more. However, now F2 is also enclosed and has to go to the right. This means the line from I3 must go to the right, so that the line from I4 must also go to the right, and so on . . .
TAKE A STEP BACK
Look at the bigger picture every now and then
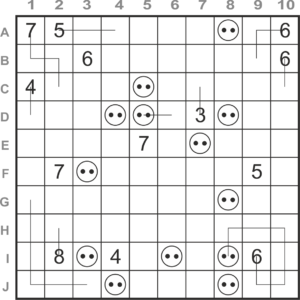
The corners are solved. What now? It often pays to look at the bigger picture, to check whether a particular possibility creates an impossibility elsewhere. The 5 in A2 can be connected to three outlets, but two of them are even numbers. So the line runs from A2 to A8.
The 4 in C1 can only be connected to outlet F3, but how? If the line were to run through D2, A1’s 7 would have to run in such a way that B3’s 6 would be trapped because it can no longer run through A3. So the 4 runs through E1 and E2. The 7 of A1 now runs via D2 to C4 (we don’t know to which outlet yet), after which the 6 of B3 must be connected to outlet D8.
We can now proceed to extend the two 6’s at the top right step by step, as discussed earlier.
FINALLY
There is much more to think about, but the tips above will set you off on the right path. You will undoubtedly discover what else is needed by yourself.
It is mainly a matter of searching, looking carefully and working accurately. If necessary check all numbers and outlets one by one. And never draw a line anywhere unless it is the only possible option.
Often it is a step-by-step process, starting at the corners. And if you get stuck, look at the bigger picture, are numbers or outlets embedded, can the line run from a number in only one way?
Lots of fun!
The above is a slightly edited version of the How-To in our books Contact ●●, ●●● and ●●●● (hard), available in Dutch on this website, and in English at www.amazon.com/author/peterritmeester.
ABC
The Rules: Enter in each row and column the letters A, B and C in such a way that no row or column contains the same letter twice. The pointing letters outside the grid indicate what letter is encountered first from the direction of the arrow.
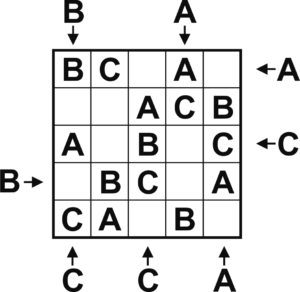
This is the solution of the puzzle we will be solving. Because only three letters are entered, two spaces remain empty in each row and column. Those two spaces could also be the first or last two in that row or column. Therefore a letter can be one, two or three spaces away from its pointing letter, but not four, because that would mean three empty spaces.
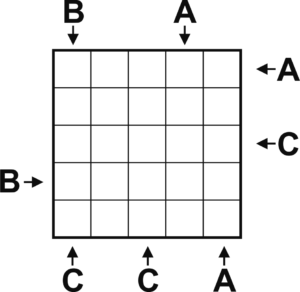
The puzzle. Where to start? Often it helps to start where two different letters appear at a corner.
The C in the leftmost column cannot be in the first two spaces from the top, because those are too far away from the pointing C below. And not in the middle, because that space is too far away from the pointing C at the right. Right next to the pointing B is also not allowed, so the C has to be in the corner at the bottom left.
There cannot be two C’s in the same row, so the space below in the middle above the pointing C remains empty. Looking at the B at the left: the first space is not possible because that is too far from the B at the top. Not the third either, because the C at the bottom is pointing at that space now, so the B has to go to the second space.
Because of this B, there is only one place left for a B in the rightmost column: three spaces of that column are pointed at by an A or C, and in the second row is already a B. The result:
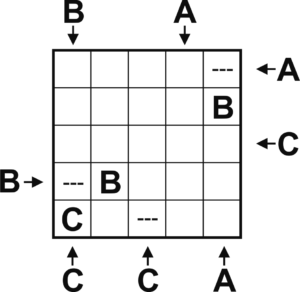
In the second row from below, the A cannot go in the middle because of the pointing C below, and not in the space next to it, because that is too far from the pointing A at the top, so it has to go to the far right.
The only place for a C in the rightmost column is now in the middle, right next to the pointing C at the right. There is only one place left for a B in the bottom row, and after that just one place for the A:
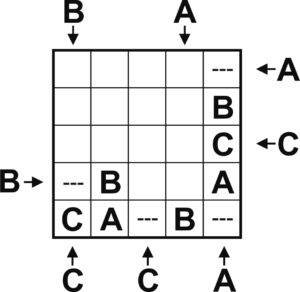
The B in the leftmost column has to be in the first space: the second row already has a B, and if the B would be in the middle, there would be no space left for an A in that column.
We have four B’s now. leaving just the center space for the fifth B. The space below that now has to contain a C .
We have four C’s now, leaving for the fifth C only the space in the second row, fourth column:
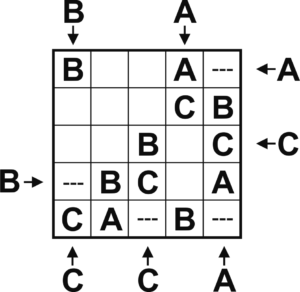
We leave the rest to you!
